Skeleton plot data is basically created according to the subroutine SKEL1 in John Philip Cropper: Tree-Ring skeleton plotting by computer in Tree-Ring Bulletin, Vol. 39, 1979 available at the The Tree-Ring Society, (Look for "Tree-Ring Bulletin and Tree-Ring Research", or try this link.) though there are indeed some small differences as described below.
The high pass filter
Before the actual skeleton marker calculations, the ring width curve is (optionally) fed through a high-pass filter, i.e. the low frequency components of the curve are removed.
Each ring width value is then divided with the mean value of a wide frame containing the surrounding ring widths.
The algorithm tries to center that frame around the ring to be filtered.
With a frame width of 21 rings, e.g. the 31st ring width is divided by the mean value of the ring widths numbered 20-40.
At the beginning and at the end of the ring series, the frame is shrunken to center properly around the current ringindex.
Though for the very first and last values, the frame consists of either the first three values or the last three values.
The Cropper algorithm
After the optional filtering the procedure follows that of Cropper, i.e. local means and standard deviations
are calculated along the ring width curve. These values are calculated from the ring widths of the nearest neighbour rings including the middle ring itself.
(The default value of the "Neighbours frame width" is set to 5.)
Then narrow rings are selected as those being smaller than a limit calculated as
"the local mean minus a percentage of the local standard deviation".
A "skeleton value" (for marker length) is then preliminary set as the difference between that limit and the ring width itself,
i.e. the smaller the ring the higher the skeleton value.
Wide rings are selected as those wider than "the local mean plus ANOTHER percentage of the standard deviation". (Cropper uses the same percentage as when selecting narrow rings!).
The function then looks for the greatest preliminary skeleton value, amax.
All skeleton values are then scaled by dividing them by amax, so their range becomes 0.01 to 1
Any zero rings are considered as a "gap" (given the skeleton value 0) which is plotted as one or more "Z" by the screen skeleton plotting mechanisms in CDendro.
"Normal rings" (neither wide nor narrow) are then given the skeleton value = -0.2
Wide rings are given the skeleton value = -0.6
The skeleton data array now contains skeleton marker values in the range 0.01 to 1, values for wide rings (=-0.6) and values for "normal" rings (=-0.2).
When the skeleton is plotted, wide rings are marked with a "b" in the diagrams.
Skeleton data can also be plotted as a curve. The horizontal lines then correspond to the wide and normal ring values.
Skeleton Chi2
During correlation operations the sample data is compared with the reference data at every possible position, i.e. the sample is shifted along the reference while correlation values are calculated at each step. A chi-square ("Chi2") analysis (Burt and Barber 1996) is then also done when enabled by CDendro settings (see below).The Chi2 analysis is done by counting the occurencies of narrow ring hits narrow ring, wide ring hits wide ring, narrow hits wide and wide hits narrow. (I.e. the actual height of the skeleton markers are not considered here, the pure existence of a marker means "this ring is narrow".) "Normal" and "wide" rings are considered the same type of ring (i.e. wide).
The Chi2 value is then calculated according to a formula where actual hits are compared to expected hits when there had been no correlation/dependence between the two curves.
For a description of The Chi Square Statistic, see e.g. http://math.hws.edu/javamath/ryan/ChiSquare.html
The CDendro code for this calculation is published at the end of this section.
Skeleton correlation
When enabled by CDendro settings (see picture below, "Skeleton Corr coeff") a normal correlation coefficient can be calculated on Skeleton data.The values for wide rings (=-0.6) and for normal rings (=-0.2) are set by experiment to give this coefficient as good "behaviour" as possible.
To experiment somewhat with the parameters for creating skeleton data, install the settings as described below.
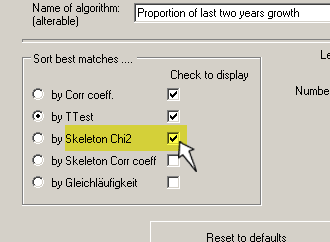
First see that you enable Skeleton plotting through the menu command
Settings/Options for normalization and matching. See that the appropriate "Check-to-display"-checkbox is checked!
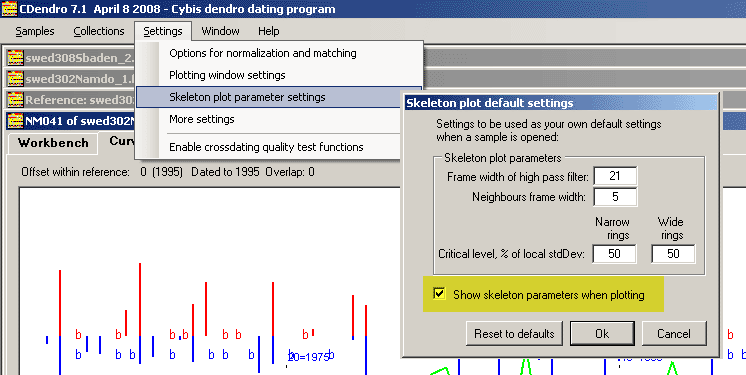
To allow for easy experimentation with parameters, see that the checkbox "Show skeleton parameters when plotting" is checked as shown above.
The skeleton plot parameters will then be visible in the lower part of the Curve display tab of a sample.
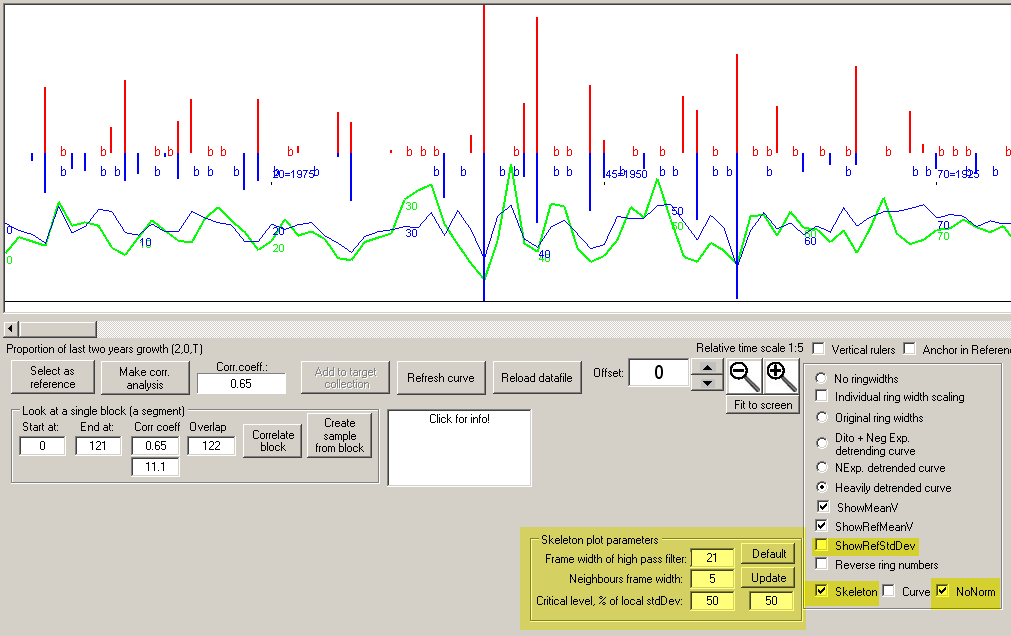
If you change the parameters of the "Skeleton algorithm" this will create more or less skeleton markers and also influence their heights.
Changed parameters will also create more or less number of "b-markers" for extra thick rings.
The algorithm follows the description by Cropper, though with this implementation we can also adjust the proportion of thick rings - Cropper had the same proportion for both thin and thick rings.
For more information about the parameters above, position your cursor over the corresponding text when running CDendro to see the "tooltips".
Now, let us compare a skeleton plot from CDendro with the pictures published in Croppers article.
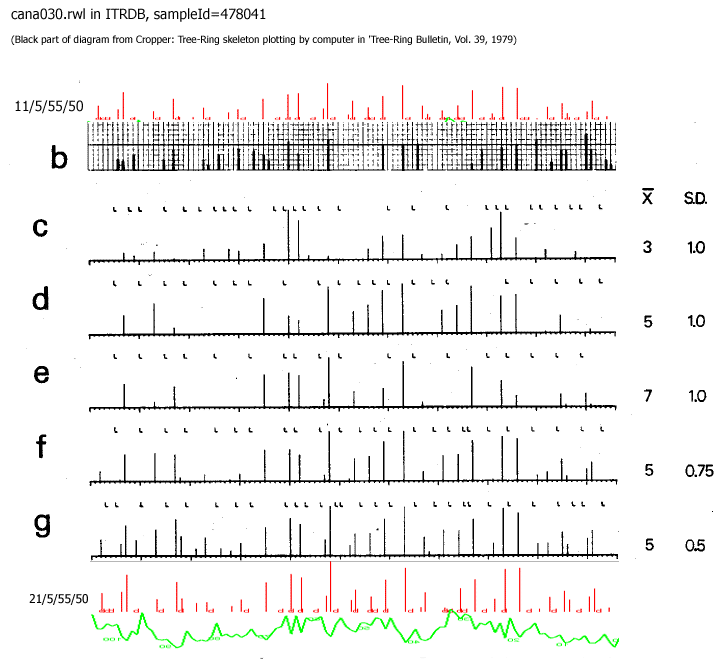
The topmost black diagram is created by a living person.
The other black diagrams are output from Croppers program when using various parameters.
The coloured diagrams come from CDendro. They differ a little from Croppers, probably because I have used another prefiltering technique than Cropper.
Public Function calcSkeletonChi2(ByRef refChain As ringChain, ByVal startIxOfSample As Integer, ByVal startIxOfREF As Integer, ByVal blockLng As Integer, ByRef becameBlockLng As Integer, ByRef actualOverlap As Integer) As Single On Error GoTo onError Dim k As Integer Dim overlapLng As Integer = 0 Dim skeletonOfSample, skeletonOfREF As Single Dim widesOrOrdinaryInRef As Integer = 0 'includes rings classified as normal or wide, i.e. skeletonvalue = iswide or skeletonvalue = isOrdinary Dim narrowsInRef As Integer = 0 ' 0 < skeletonvalue <= 1 Dim widesOrOrdinaryInSample As Integer = 0 Dim narrowsInSample As Integer = 0 ' 0 < skeletonvalue <= 1 Dim widesHitWide As Integer = 0 Dim narrowsHitNarrow As Integer = 0 Dim narrowsHitWide As Integer = 0 Dim widesHitNarrow As Integer = 0 If refChain Is Nothing Then Return 0 Dim isWide As Single = frmAlgoritm.p_skeletonWide Dim isOrdinary As Single = frmAlgoritm.p_skeletonOrdinary Dim isGap As Single = frmAlgoritm.p_skeletonNoData becameBlockLng = 0 For k = 0 To blockLng - 1 If Me.skeletonLength(k + startIxOfSample, skeletonOfSample) AndAlso refChain.mySkeleton.skeletonLength(k + startIxOfREF, skeletonOfREF) Then If skeletonOfSample <> isGap And skeletonOfREF <> isGap Then 'no zero gap in either segment overlapLng += 1 If skeletonOfREF = isWide Or skeletonOfREF = isOrdinary Then widesOrOrdinaryInRef += 1 ElseIf skeletonOfREF > 0 Then narrowsInRef += 1 End If If skeletonOfSample = isWide Or skeletonOfSample = isOrdinary Then widesOrOrdinaryInSample += 1 ElseIf skeletonOfSample > 0 Then narrowsInSample += 1 End If If skeletonOfSample = isWide Or skeletonOfSample = isOrdinary Then If skeletonOfREF = isWide Or skeletonOfREF = isOrdinary Then widesHitWide += 1 ElseIf skeletonOfREF > 0 Then widesHitNarrow += 1 End If ElseIf skeletonOfSample > 0 Then If skeletonOfREF = isWide Or skeletonOfREF = isOrdinary Then narrowsHitWide += 1 ElseIf skeletonOfREF > 0 Then narrowsHitNarrow += 1 End If End If End If becameBlockLng += 1 'includes any gaps End If Next actualOverlap = overlapLng If overlapLng = 0 Then Return 0 Dim wideFreqInRef As Single = 0 Dim narrowFreqInRef As Single = 0 If widesOrOrdinaryInRef > 0 Then wideFreqInRef = widesOrOrdinaryInRef / overlapLng If narrowsInRef > 0 Then narrowFreqInRef = narrowsInRef / overlapLng Dim wideFreqInSample As Single = 0 Dim narrowFreqInSample As Single = 0 If widesOrOrdinaryInSample > 0 Then wideFreqInSample = widesOrOrdinaryInSample / overlapLng If narrowsInSample > 0 Then narrowFreqInSample = narrowsInSample / overlapLng Dim chi2 As Single = 0 Dim expected As Single expected = wideFreqInRef * wideFreqInSample * overlapLng If expected > 0 Then chi2 = (widesHitWide - expected) * (widesHitWide - expected) / expected End If expected = wideFreqInSample * (1 - wideFreqInRef) * overlapLng If expected > 0 Then chi2 += (widesHitNarrow - expected) * (widesHitNarrow - expected) / expected End If expected = (1 - wideFreqInSample) * wideFreqInRef * overlapLng If expected > 0 Then chi2 += (narrowsHitWide - expected) * (narrowsHitWide - expected) / expected End If expected = (1 - wideFreqInSample) * (1 - wideFreqInRef) * overlapLng If expected > 0 Then chi2 += (narrowsHitNarrow - expected) * (narrowsHitNarrow - expected) / expected End If Return chi2 onError: Return 0 End Function